群論へのお誘い 附：悪魔の方向
本棚を見ると本が一冊後ろ向きに入っている。白い腹（小口）を見せているのである。昨日慌てて入れたときに背中を奥にして突っ込んでしまったのだろう。 ふーむ。本というのは本棚に正しく入れることもできるし、逆さまにもできるし、後ろ向きにもできるし、逆さまで後ろ向きにもできるのだなあ。で、元へ戻すときには、逆さまの場合はもう一度逆さまにすればいいし、後ろ向きのときはもう一度後ろ向きにすればいいし、逆さまで後ろ向きのときはもう一度逆さまで後ろ向きにすればいいのか・・・ じゃあ、逆さまにして、後ろ向きにして、もう一度後ろ向きにして、逆さまにして、後ろ向きにして、逆さまにして、もう一度逆さまにして、後ろ向きにして、逆さまにしたら、 直す時には 逆さまにして、後ろ向きにして、もう一度後ろ向きにして、逆さまにして、後ろ向きにして、逆さまにして、もう一度逆さまにして、後ろ向きにして、逆さまにしなければならないのか。 やってみたら、一回逆さまにするだけで直った。 ふーむ。いいじゃないか。もしこうじゃなかったら、自分は生きていく勇気を失うところだった。 ふつう物事はこねくり回しているうちにどんどんこんがらかって収拾がつかなくなってしまうもの ではなかったっけ？ 確認しておかなければならない。 逆さまにしてもう一度逆さまにすると、動かさなかった時と同じ状態に戻るから 整然たる世界に感謝しなければならない。 なんのことだか自分でもよく分からないので、もっと単純な話にしてみよう。
上のような升目で駒を動かす場合を考えてみる。 動＋動＝不 （動かした後もう一度動かすと、動かさなかった場合と同じになる。） 動＋不＝動 （動かした後動かさないと、一回動かしただけの場合と同じになる。） 不＋動＝動 （動かさない後動かすと、一回動かしただけの場合と同じになる。） 不＋不＝不 （動かさない後動かさないと、動かさなかった場合と同じになる。） つまりはどの動作にどの動作を組み合わせても、結果は単純な動か不かと同じになるのである。 動不 さて一体この話に何の意味があるというのだ・・・とあなたは言うだろう。 電灯にスイッチの紐がぶら下がっている。あなたはその下にいる。あなたに許された選択肢は「引っ張る」と「引っ張らない」の二つである。 ちょっとシーンとしてしまったので、話をひとつ複雑にしてみる。
上のように升目を増やして同じように考えてみる。 縦＋縦＝不 つまり 縦横斜不 となる。どうもこれは冒頭の本棚の話と同じ構造になっているらしい。確かにどれとどれを組み合わせても縦・横・斜・不のどれか一つと同じことになってしまうのだ。 （もの足りない人は升目を上下二段に重ねた立体にしてみよう。選択肢は八個、式は六十四個できるはずである。） ところで、上の升目の例はちょっと見方を変えると（45゜回転させてみると）
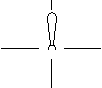
このような四方向に倒せるレバーの動きと同じと捉えることもできる。（動かすときは一旦垂直に起こしてから任意の方向へ倒す。） この場合は考えられる動かし方は「現在位置より一つ右（時計が進む方向）へ」、「左（時計が戻る方向）へ」、「反対側へ」、「そのまま」、とも表現できることになる。 右＋右＝反 右左反不 である。またここでは 右＋右＋右＝左 などともなる。 さて、上に図示した何れのケースでも位置の変化について次のことが言える。 ●どんな変化が組み合わされてもその結果はある一つの変化の結果と同じになる。 たとえばレバーの例で見ると 右左反不 のように、表に示された結果は右・左・反・不の4つに限られている。 つまり、何れのケースでも、 どんな変化をどのようにいくつ積み重ねても その結果がとんでもない想定外の結果を招いて収拾がつかなくなる という事態は起こり得ないのだ。これらの動作や操作の世界においては、いくつかの変化のし方を要素として、それらの要素が過不足なく全て適切に関係付けられているからである。これは整然たる自己完結体系といってよいだろう。 要素の数（変化の種類）を増やしてみよう。
（図は左右にずっと続いている想定） いま、任意の位置から右へ一つ動く変化を「1」と名付けよう。 例えば「1」という要素に「2」という要素が加わると、「3」という要素と同じになる。「3」と「4」では「7」と同じになる。 もうお気付きと思うが、これは普通の「整数の足し算・引き算」ではないか。 さて、「整然たる自己完結体系」の内容をもうすこしはっきりと規定してみよう。 1．どの要素とどの要素を組み合わせることも可能で、その結果自体も一個の要素として体系内に存在する。 整数の足し算・引き算の世界はこれらの条件を満たしているので整然たる自己完結体系であるということができる。我々が行おうとする如何なる足し算・引き算もが必ず成功裏に成立すると我々が信ずることができるのは、この極めて整然とした体系の保証によるのである。（整数の範囲を越えた実数や複素数の足し算・引き算でも同じことである。） 足し算・引き算で結合法則が成り立つのは明らかだが、上記の
の世界ではどうだろう。指で動きをなぞって考えてみよう。
の世界も見よう。 なるほどこういう風になっているのか。経路が違っても到達点は同じなのだ。面白い！ 整数の掛け算の世界は整然たる自己完結体系だろうか。 （以上のことから、整数は知っているが分数を知らない児童の理解する掛け算の世界は完全ではなく、また分数の掛け算さえ知っていれば「0」を掛けることができなくても一定の整然とした世界を把握しているのだと言ってよいようだ。） さて、そろそろまとめよう。 数学らしく表現すると、ある集合の任意の元について、ある二項演算が次の条件を満たすとき、その集合はその演算について群をなす、と言う。 上に述べた足し算・引き算や掛け算、また冒頭から書いてきた本棚への本の入れ方やレバーの動かし方という具体的動作の話においても、何が単位元で、どれがどれの逆元かということについてはもう十分にお分かりだろうと思う。 結局、私は数学的概念の「群」は単なる数学上の無味な概念ではなく、われわれの住むこの世界の整然さの理由を説明する、一見奇妙だがスッキリした表現法なのであるということを長々と説明してきたことになるらしいのだが、どうだろう、そのように理解していただけただろうか。 （この宇宙において我々が混乱もなく思考したり行動したりできるのは、果たしてこの宇宙がもともと整然とした振る舞いをするように出来ているからなのか、あるいは我々の脳が混沌とした宇宙の振る舞いの中に仮想的に整然とした秩序をでっち上げているからなのかは、私にはわからない。 しかし我々がこの世界の仕組みを一定の秩序あるものだと認識できている限り、それは願ってもないことだ。様々な複雑な現象や事実や抽象概念についてその仕組みの中に群の存在をもし見つけることができたなら、それは我々がその仕組みをこんがらかることのない整然としたものとして把握できたということを意味する。群の性質について調べる研究の実用的有用さを説明しろと言われたらそういうことになるだろう。数学の理解は群の概念無くしては立ち行かない。） 附録： 悪魔の方向 （この項は、今にして思えば若き織田孝幸氏との交友の賜物である。）
|
だから不である。
で、結果は同じ不になった。 成り立つ。
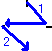だから反だ。
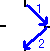と、これも反になる。成り立つ。